Stosunki

Podział zbioru w stosunku \$a:b\$

Stosunek liczb dodatnich \$a,b\in\mathbb{N_+}\$ określamy następująco. \[ a:b \Leftrightarrow \left(\frac{a}{b}= \frac{x}{y} \ \ oraz \ \ x+y=m \right) \]

gdzie liczby \$a\$ i \$b\$ są w postaci nieskracalnej i odzwierciedlają podział pewnego zbioru, gdzie jego całość, to pewna liczba dodatnia \$m\$.

W klasie uczy się \$24\$ uczniów, gdzie 6 uczniów to chłopcy, a \$18\$ uczniów to dziewczęta. Jaki jest stosunek chłopców do dziewcząt?

x=6: liczba chłopców w klasie

y=18: liczba dziewcząt w klasie

x+y=24: liczba uczniów w klasie

\[ \frac{x}{y} = \frac{6}{18} = \frac{1}{3} \]

Odp: Stosunek chłopców do dziewcząt wynosi \$1:3\$. Można powiedzieć, że na troje dziewczyn, przypada jeden chłopiec.

Zauważmy, że \$\frac{1}{3}*24 = 8 \neq \$ liczby chłopców w klasie. Jest tak, bo stosunki pokazują relację między częściami dzielącymi zbiór, a nie częścią i całością zbioru.

W klasie uczy się \$20\$ uczniów. Stosunek chłopców do dziewcząt wynosi \$2:3\$. Ile chłopców i dziewcząt uczy się w tej klasie?

x:liczba chłopców

y:liczba dziewcząt

x+y:liczba uczniów w klasie

Rozwiązujemy układ równań z dwoma niewiadomymi: \[ \frac{x}{y} = \frac{2}{3} \wedge x+y=20 \] Przekształcając otrzymujemy: \[\begin{cases} 3x=2y \\ x+y= 20 \end{cases}\]

\[\begin{cases} 3(20-y)= 2y \\ x = 20-y \end{cases} \Leftrightarrow \begin{cases} 60-3y = 2y \\ x = 20-y \end{cases} \] \[\begin{cases}60=5y \\ x=20-y \end{cases} \Leftrightarrow \begin{cases} y=12 \\ x=8 \end{cases} \]

Odp: Ilość chłopców w klasie to \$8\$, a dziewcząt to \$12\$.

W praktyce obliczamy stosunki szybciej, bez rozwiązywania układu równań szukając takiego \$k\in\mathbb{N_+}\$, że:

\[ \frac{a}{b}=\frac{ka}{kb} = \frac{x}{y} \wedge ka+kb=m \]

W klasie uczy się \$20\$ uczniów. Stosunek chłopców do dziewcząt wynosi \$2:3\$. Ile chłopców i dziewcząt uczy się w tej klasie?

2x:liczba chłopców

3x:liczba dziewcząt

2x+3x:liczba uczniów w klasie

\[\begin{align*} 2x+3x &= 20 \\ 5x&=20 \\ x&=4 \end{align*}\]

Odp: Ilość chłopców w klasie to \$8\$, a dziewcząt to \$12\$.

Obwód prostokąta wynosi \$42\$. Stosunek boku krótszego do dłuższego prostokąta wynosi \$3:4\$. Oblicz pole tego prostokąta.

3x:krótszy bok

4x:dłuższy bok

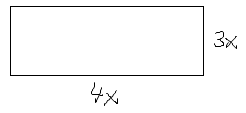
Pole prostokąta: \$3x*4x=12x^2\$.

Z równania na obwód wyliczamy \$x\$:

\[\begin{align*} 2(3x + 4x) &= 42 \\ 2*7x&=42 \\ 14x&=42 \\ x&=3 \end{align*}\]

Obliczamy pole:

\[ 12*3^2 = 12*9 = 108 \]

Odp: Pole prostokąta wynosi \$108\$.

Spis treści

Stosunki

Podział zbioru w stosunku \$a:b\$