Liczby rzeczywiste - suma zbiorów liczb wymiernych i niewymiernych
Liczby wymierne
Liczby wymierne i ich zbiór \$\mathbb{Q}\$, to liczby, które możemy zapisać w postaci ułamka. O to przykładowe liczby wymierne.
\[ \frac{1}{2} \qquad -\frac{7}{99} \qquad 0.0173 \qquad \sin(30\degree) \qquad \log_3(27) \]Chodź działania na liczbach wymiernych intuicyjnie wydają się zrozumiałe, w świecie fizycznym możemy dokonać pomiaru tylko z określoną dokładnością. Na przykład liczba \$\frac{1}{3}\$ ma rozwinięcie dziesiętne nieskończone okresowe i na kalkulatorze mamy przybliżenie tej liczby.
\[ \frac{1}{3} = 0.(3) = 0.33333... \]Liczby niewymierne
Zbiór liczb niewymiernych oznaczamy przez \$\mathbb{I}\$ (duża litera I). Liczba niewymierna to liczba której nie możemy przedstawić w postaci ułamka.
Z Twierdzenia Pitagorasa, jeśli mamy trójkąt prostokątny z bokami \$a\$ i \$b\$ oraz przeciwprostokątną \$c\$, to suma kwadratów boków jest równa kwadratowi przeciwprostokątnej.
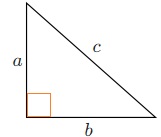\[ c^2=a^2+b^2 \]
Niech \$a=1\$ oraz \$b=1\$, mamy \$c^2=1^2+1^2 = 2\$. Mamy do rozwiązanie równanie \$c^2=2\$. Pytanie, ile wynosi \$c\$? Możemy założyć, że \$c>0\$.
Otóż, już starożytni udowodnili, że nie ma takich liczb całkowitych \$x,y\$, że:
\[ \left(\frac{x}{y} \right)^2=2 \]Skoro liczba \$c\$ nie jest wymierna, to możemy zapytać jak przedstawić wielkość tej liczby? Przecież odcinek \$c\$ ma jakąś długość.
Definiujemy zbiór liczb rzeczywistych i jego własności a zbiory liczb wymiernych i niewymiernych są podzbiorami tego zbioru.
Równanie \$c^2=2\$ w postaci pierwiastka:
\[ c^2 = 2 \ \text{wtedy i tylko wtedy, gdy} \ \sqrt{2} = c, \quad \text{dla} \quad c\in\mathbb{R}, c\ge 0 \]Tak więc \$\sqrt{2}\$ jest liczbą niewymierną.
Przyblizenie \$\sqrt{2}\$ do czwartego miejsca dziesiętnego z niedomiarem: \$\sqrt{2} \approx 1.4142\$.
Szukamy przybliżenia \$\sqrt{2}\$.
\[ \begin{aligned}\left(\frac{11}{10}\right)^2 < \left(\frac{12}{10}\right)^2 < \left(\frac{13}{10}\right)^2 < \left(\frac{14}{10}\right)^2 < \ &2 \ < \left(\frac{15}{10}\right)^2 \\ \left(\frac{141}{100}\right)^2 < \ &2 \ < \left(\frac{142}{100}\right)^2 \\ \left(\frac{1411}{1000}\right)^2 < \left(\frac{1412}{1000}\right)^2 < \left(\frac{1413}{1000}\right)^2 < \left(\frac{1414}{1000}\right)^2 < \ &2 \ < \left(\frac{1415}{1000}\right)^2 \\ \left(\frac{14141}{10000}\right)^2 < \left(\frac{14142}{10000}\right)^2 < \ &2 \ < \left(\frac{14143}{10000}\right)^2 \end{aligned}\]Liczby rzeczywiste
Zbiór liczb rzeczywistych oznaczamy \$\mathbb{R}\$.
W wyrażeniach algebraicznych, jeśli nie zaznaczono inaczej, to liczby które możemy podstawić za niewiadome, które występują w tych wyrażeniach należą do zbioru liczb rzeczywistych.
Suma liczby wymiernej i niewymiernej należy do zbioru liczb niewymiernych. Np. \$(1+\sqrt{2})\in\mathbb{I}\$.
Załóżmy, że suma ta jest wymierna i że \$w\in\mathbb{Q}\$, \$n\in\mathbb{I}\$.
\[ \large \begin{aligned} w+n&=\frac{p}{q} \\ \frac{a}{b} + n &= \frac{p}{q} \\ n=\frac{p}{q} - \frac{a}{b} &= \frac{bp -aq}{bq} \Rightarrow contr. \end{aligned} \]Otrzymaliśmy sprzeczność z założeniem, a zatem suma liczby wymiernej i niewymiernej nie może być wymierna, więc jest niewymierna.
Iloczyn liczb niewymiernych, może być liczbą wymierną, np. \$\sqrt{2} * \sqrt{2} = \left(\sqrt{2}\right)^2 = 2 \$.
Zbiór \$\mathbb{R}\$ pokrywa na osi liczbowej wszystkie możliwe wartości na których operujemy w szkole.