Działania na zbiorach
Podzbiór zbioru
Zbiór \$A\$ nazywamy podzbiorem zbioru \$B\$ wtedy i tylko wtedy, gdy każdy element należący do zbioru \$A\$ należy także do zbioru \$B\$.
Ilustracja:
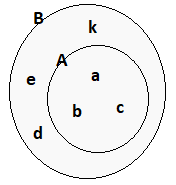
Zapisujemy to jako \$A\subset B\$. Mówimy też zbiór \$A\$ zawiera się w zbiorze \$B\$.
Dla zbiorów liczbowych mamy następujące zawierania:
\[ \mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q} \subset\mathbb{R} \]oraz
\[ \mathbb{I}\subset \mathbb{R} \]Niech \$A=\{ 5, 7, 9, 3 \}\$, \$B=\{ 7, 9 \}\$ oraz \$C=\{ 3,5,9,7,8 \}\$. Wtedy:
\[ A\subset C \] \[ B\subset A \quad \text{oraz} \quad B\subset C \]Zauważmy dla dowolnych zbiorów \$A\$ i \$B\$, gdy \$A\subset B\$ oraz \$B\subset A\$, to mamy równość zbiorów \$A=B\$. Wynika to wprost z definicji równości i podzbioru zbioru. Popatrzmy na poniższy przykład.
Niech \$X=\{ x\in\mathbb{N}: x^2\le 9\}\$ oraz \$Y=\{ 0, 1, 2, 3 \}\$. Mamy \$X=Y\$, ale też \$X\subset Y\$ i \$Y\subset X\$.
W poniższych definicjach wyrażenie \$\{x: warunek\}\$ oznacza zbiór spełniający określony warunek, a \$x\$ pochodzi (niejawnie) z pewnej przestrzeni (zbioru). Krótko mówiąc zbiory w podanych definicjach są podzbiorami tej przestrzeni.
Suma zbiorów
Sumą zbiorów \$A\$ i \$B\$ nazywamy zbiór do którego należą elementy ze zbioru \$A\$ lub ze zbioru \$B\$.
\[ A\cup B = \{x: x\in A \ \text{lub} \ x\in B \} \]Ilustracja:

Niech \$A=\{a,b,c\}\$ i \$B=\{0,1,2,3,4,5,6,7,8,9\}\$. Wtedy \$A\cup B=\{ a,b,c, 0,1,2,3,4,5,6,7,8,9 \}\$.
\$\mathbb{Z_{-}} \cup \mathbb{Z_{+}} \cup \{0\} = \mathbb{Z} \$ .
Niech \$X=\{ x\in\mathbb{N}: x^2< 9\}\$ oraz \$Y=\{x\in\mathbb{Z}: -3 < x\le 9 \}\$. Szukamy zbioru \$X\cup Y\$. Wypiszmy elementy zbiorów \$X\$ i \$Y\$.
\$X=\{ 0, 1, 2 \}\$ oraz \$Y=\{ -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 \}\$. Bierzemy elementy należące do zbioru \$X\$ lub zbioru \$Y\$:
\[ X\cup Y = \{ -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 \} \]Niech \$A=\{a,b, c, d\}\$, \$B=\{ c, h, i, j, k \}\$, \$C=\{ a, i, j, y, z\}\$. Wtedy:
\$A\cup B = \{ a,b,c,d,h,i,j,k \}\$
\$A\cup C = \{ a,b,c,d,i,j,y, z \}\$
\$B\cup C = \{ a,c,h,i,j,k,y,z \}\$
\$A\cup B\cup C = \{ a,b,c,d, h,i,j,k,y,z \}\$
Iloczyn zbiorów
Iloczynem zbiorów (część wspólną) \$A\$ i \$B\$ nazywamy zbiór do którego należą elementy ze zbioru \$A\$ oraz ze zbioru \$B\$.
\[ A\cap B = \{x: x\in A \ \text{i} \ x\in B \} \]Ilustracja:
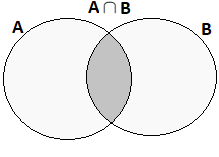
Zbiory \$A\$ i \$B\$ są rozłączne, gdy nie mają części wspólnej, to jest, gdy \$A\cap B=\emptyset\$.
Niech \$A=\{a,b,c\}\$ i \$B=\{0,1,2,3,4,5,6,7,8,9\}\$. Wtedy \$A\cap B= \emptyset\$.
\$\mathbb{R_{+}} \cap \mathbb{N} = \mathbb{N_{+} } \$ .
Niech \$X=\{ x\in\mathbb{N}: x^2< 9\}\$ oraz \$Y=\{x\in\mathbb{Z}: -3 < x\le 9 \}\$. Szukamy zbioru \$X\cap Y\$. Wypiszmy elementy zbiorów \$X\$ i \$Y\$.
\$X=\{ 0, 1, 2 \}\$ oraz \$Y=\{ -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 \}\$. Bierzemy elementy należące do zbioru \$X\$ oraz zbioru \$Y\$:
\[ X\cap Y = \{ 0,1,2 \} \]Niech \$A=\{a,b, c, d, k\}\$, \$B=\{ a, d, c, h, i, j, k \}\$, \$C=\{ a, i, j, y, z, k\}\$. Wtedy:
\$A\cap B = \{ a, c, d, k \}\$
\$A\cap C = \{ a, k \}\$
\$B\cap C = \{ a, i, j, k \}\$
\$A\cap B\cap C = \{ a,k \}\$
Różnica zbiorów
Różnicą zbiorów \$A\$ i \$B\$ nazywamy zbiór do którego należą elementy ze zbioru \$A\$ oraz nie należą do zbioru \$B\$.
\[ A\setminus B = \{x: x\in A \ \text{i} \ x\notin B \} \]Ilustracja:
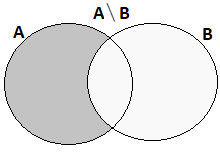
Niech \$A=\{a,b,c, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}\$ i \$B=\{0,1,2,3,4,5,6,7,8,9\}\$. Wtedy:
\$A\setminus B= \{a,b,c \}\$
\$B\setminus A= \emptyset \$
Różnica zbiorów nie jest przemienna. Dla zbioru \$B\setminus A\$ nie ma takiego elementu, który należy do \$B\$ i jednocześnie nie należy do \$A\$.
Niech \$A=\{ 1,2,3,4 \}\$, \$B=\{ 4,5,6,7,8,9 \}\$. Wtedy \$A\setminus B=\{ 1,2,3 \}\$ oraz \$B\setminus A=\{ 5,6,7,8,9 \}\$.
Niech \$A=\{ 10, 20, 30 \}\$, \$B=\{ 40, 50, 60 \}\$. Wtedy \$A\setminus B=A\$ oraz \$B\setminus A=B\$.
Niech \$A=\{ a,b,c,d \}\$, \$B=\{a,b \}\$. Wtedy \$A\setminus B=\{ c,d \}\$ oraz \$B\setminus A=\emptyset\$.
Dla zbiorów liczbowych mamy przykładowe zależności:
\$\mathbb{R}\setminus \mathbb{I} = \mathbb{Q} \$
\$\mathbb{Z}\setminus \mathbb{N} = \mathbb{Z_{-}} \$
Dopełnienie zbioru
Dopełnienie zbioru \$A\$ w pewnej przestrzeni (zbioru) \$\Omega\$, to różnica tej przestrzeni i zbioru \$A\$ przy założeniu, że \$A\subset \Omega\$.
\[ A^{'}=\Omega \setminus A \]Ilustracja:
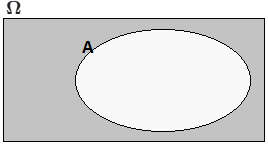
Dla przestrzeni równej zbiorowi liczb rzeczywistych \$\mathbb{R}\$ dopełnieniem zbioru liczb \$\mathbb{I}\$ jest zbiór \$\mathbb{Q}\$.
\[ \mathbb{I^{'}}=\mathbb{R}\setminus \mathbb{I} = \mathbb{Q} \]Dla przestrzeni równej zbiorowi liczb naturalnych \$\mathbb{N}\$ dopełnieniem zbioru liczb \$\mathbb{N} \$ z wyjątkiem liczby \$7\$ jest liczba \$7\$.
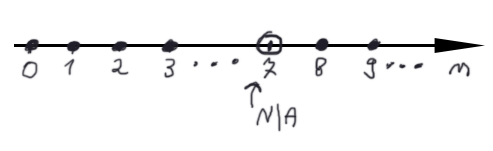
Przestrzeń: \$\mathbb{N}\$ - oś liczbowa
\$A=\mathbb{N}\setminus \{7\}\$ - zbiór zaznaczony na osi
\$A^{'}=\mathbb{N}\setminus A\$ - dopełnienie zbioru \$A\$
Podzbiór zbioru \$X\$: Zbiór którego wszystkie elementy są także w zbiorze \$X\$.
Suma zbiorów \$A\$ i \$B\$: Zbiór zawierający niepowtarzające się elementy ze zbiorów \$A\$ i \$B\$.
Iloczyn zbiorów \$A\$ i \$B\$: Zbiór który jest częścią wspólną zbiorów \$A\$ i \$B\$.
Różnica zbiorów \$A\$ i \$B\$: Zbiór który ma elementy ze zbioru \$A\$, które nie są w zbiorze \$B\$.
Dopełnienie zbioru \$X\$: Różnica przestrzeni (zbioru) \$\Omega\$ oraz zbioru \$X\$.
Kolejność działań
Kolejność działań na zbiorach jest umowna i następująca:
Wykonujemy kolejno: dopełnienie zbioru, iloczyn zbioru, na końcu sumę zbioru, chyba, że w wyrażeniach występują dodatkowe nawiasy.
Poniższe dwa wyrażenia są równoważne.
\[ A \cup B \cap C \] \[ A \cup (B \cap C) \]Możemy zmienić kolejność działań stosując nawiasy. Poniżej najpierw obliczamy sumę zbiorów, a później ich iloczyn.
\[ (A \cup B) \cap C \]