Wartość bezwzględna - wprowadzenie
Definicja
Dla nieujemnej liczby opuszczamy po prostu ||, a dla wartości ujemnej opuszczając te znaki zmieniamy znak liczby na przeciwny. A więc dla każdego \$a\in\mathbb{R}\$ mamy \$|a|\ge 0\$.
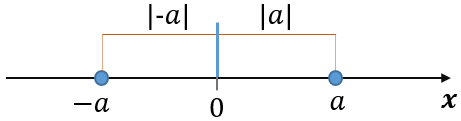
Wartość bezwzględną możemy interpretować jako odległość liczby \$a\$ od zera na osi liczbowej. Taka interpretacja ułatwia także rozwiązywać niektóre równania i nierówności z wartością bezwzględną.
Kilka przykładów z wartości bezwzględnej.
\$|15| = 15\$
\$|-97| = 97\$
\$\displaystyle{\left|\frac{7}{5}\right| = \frac{7}{5}}\$
\$|-\sqrt{2}| = \sqrt{2}\$
Z pomocą kalkulatora przybliżamy \$\sqrt{2} \approx 1.4 > 1 \$, a więc wyrażenie \$1-\sqrt{2}< 0 \$. Opuszczamy wartość bezwzględną ze zmianą znaku.
\[\begin{aligned} |1-\sqrt{2}| &= -(1-\sqrt{2}) \\ &= -1+\sqrt{2} \\ &\approx 0.4 \end{aligned}\]Wzory
Podstawowe prawa działań z wartością bezwzględną dla \$a,b\in\mathbb{R}\$.
\[ |a*b|=|a|*|b| \] \[ \left|\frac{a}{b}\right| = \frac{|a|}{|b|} \ \text{dla} \ b\neq 0 \] \[ |a-b|=|b-a| \] \[ |a^2|=|a|^2 = a^2 \] \[ \sqrt{a^2} = |a| \]\$|7-5|=|2|=|5-2| = |-2|\$
\$|39-15|=|24|=|15-39| = |-24|\$
\$|-8-(-3)|=|-5|=|-3-(-8)| = |5|\$
\$\sqrt{2^2}=\sqrt{4} = 2 = |2|\$
\$\sqrt{(-2)^2}=\sqrt{4} = 2 = |-2|\$
\$\sqrt{7^2}=\sqrt{49} = 7 = |7|\$
\$\sqrt{(-7)^2}=\sqrt{49} = 7 = |-7|\$
\$\sqrt{x^2}=x, \ \text{dla} \ x\ge 0\$
\$\sqrt{x^2}=|x|, \ \text{dla} \ x\in\mathbb{R} \$