Przedziały liczbowe
Definicja
Przedziały liczbowe definiujemy jako zbiory:
Przedziały ograniczone:
\$\displaystyle{ (a;b) = \{ x\in\mathbb{R}: a < x< b \} }\$
\$\displaystyle{ [a;b] = \{ x\in\mathbb{R}: a \le x\le b \} }\$
Przedziały z nieskończonością (nieograniczone):
\$\displaystyle{ (-\infty;\infty) = \mathbb{R} }\$
\$\displaystyle{ (-\infty;b) = \{x\in\mathbb{R}: x< b \} }\$
\$\displaystyle{ (-\infty;b] = \{x\in\mathbb{R}: x\le b \} }\$
\$\displaystyle{ (a;\infty) = \{x\in\mathbb{R}: x>a \} }\$
\$\displaystyle{ [a;\infty) = \{x\in\mathbb{R}: x\ge a \} }\$
Przedziały \$[a;b) \$ i \$(a;b] \$ definiujemy odpowiednio.
Na przedziałach wykonujemy te same działania co na zbiorach.
Przedział liczbowy, to zbiór zawierajacy wszystkie liczby rzeczywiste w określonym przedziale.
Przedział otwarty \$(a;b)\$, to zbiór w którym skrajne elementy przedziału się nie zawierają.
Przedział domknięty \$[a;b]\$, to zbiór w którym skrajne elementy przedziału są zawarte.
Zaznaczanie przedziałów na osi liczbowej
Na rysunku zaznaczono przedział \$\bigl(-5; 7\bigr)\$, który jest obustronnie otwarty.
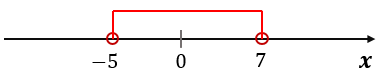
Kółka otwarte oznaczają, że wartości końcowe nie są częścią przedziału.
Na rysunku zaznaczono przedział \$\bigl[-2; 13\bigr]\$, który jest obustronnie domknięty.
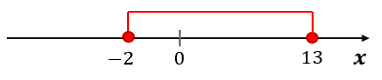
Kółka zamknięte oznaczają, że wartości końcowe są częścią przedziału.
Na rysunku zaznaczono przedział \$\bigl(-2; 13\bigr]\$.
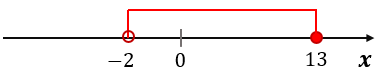
Przedział jest prawostronnie domknięty.
Na rysunku zaznaczono przedział \$\bigl[-11; 5\bigr)\$.

Przedział jest lewostronnie domknięty.
Na rysunku zaznaczono przedział \$\bigl(-5; \infty)\$.
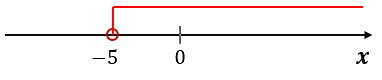
Przedział jest prawostronnie nieograniczony.
Na rysunku zaznaczono przedział \$\bigl(-\infty; -2\bigr)\$.
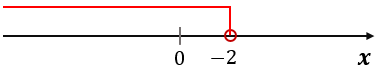
Przedział jest lewostronnie nieograniczony.
Na rysunku zaznaczono przedział \$\bigl[3; \infty\bigr)\$.
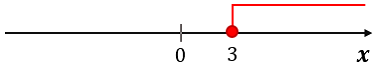
Przedział jest lewostronnie domknięty i prawostronnie nieograniczony.
Na rysunku zaznaczono przedział \$\bigl(-\infty; 3\bigr]\$.
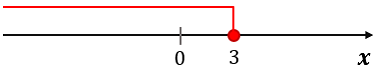
Przedział jest prawostronnie domknięty i lewostronnie nieograniczony